Dos mil años después de Sócrates, el francés Descartes (1596-1650), diseñó otro método para acercarse a la verdad, utilizando el modelo matemático. Es un procedimiento que ha caracterizado a la ciencia natural desde el siglo XVII.
El primer obstáculo proviene del propio uso coloquial del lenguaje. Se habla de guitarra clásica española, para distinguirla de la flamenca. Se clasifica una guitarra como profesional o de concierto y otras de semiprofesional para estudio distinguiendo las fabricadas de manera artesanal o parcialmente en serie.
Una fábrica que produce 20.000 guitarras al año puede incluir en su catálogo guitarras que denomina profesionales y tener en su plantilla guitarreros de renombre y guitarreros que fabrican en solitario 20 al año y por encargo puede construir guitarras de estudio, que también denomina semiprofesionales.
La confusión aumenta cuando al solicitar una guitarra en una tienda de instrumentos musicales, encontramos una gama amplia por unos 50€, otra entre 100 y 300€ y otra más por 500€-1000€. La mayoría de guitarrerías tradicionales ofrecen su producto: guitarras de alta gama o de concierto por 2.000 a 15.000€.
No es exclusivo de la guitarra, pero siendo un instrumento tan popular, hay tantas versiones como niveles adquisitivos de los compradores.
Una flauta dulce o de pico de tonalidad soprano de plástico puede costar 10€ una de madera 30-80€, de ébano 300€. Podemos encontrar flautas de pico llamadas de alta gama por 1000 hasta 3000€ y más. Un coleccionista puede pagar cifras muy superiores por un ejemplar antiguo.
La publicidad ofrece “guitarras para el intérprete más exigente, que demanda la máxima calidad y lo más cercano a la perfección como se pueda conseguir en un producto realizado a mano”.
¿En la fabricación de una guitarra clásica española hay operaciones que no se pueden conseguir con igual precisión y calidad si los hace una máquina?.
Normalmente las máquinas trabajando en salas aclimatadas. Logran sin dificultad reproducciones con grados de precisión de cotas del orden de las milésimas. Algo fuera del alcance de la capacidad de los medios de medición de los que dispone un guitarrero.
Otra evidencia científica es que así como se pueden realizar formulaciones químicas idénticas pesando con precisiones de millonésima de gramo los componentes que van a constituir una cerámica o un vidrio, resulta del todo punto imposible lograr que la madera de dos árboles de la misma especie sean idénticos. La variabilidad es una propiedad que asegura la supervivencia de los organismos vivos.
Quienes practican la talla en madera saben lo diferente que puede ser la dureza y comportamiento al corte con la gubia que presentan la madera de dos tablones de la misma especie arbórea, aun proviniendo de la misma plantación. Las mediciones de resistencia a la compresión, tracción, módulo de elasticidad, dureza, nivel sonoro etc., son muy diferentes aunque tengamos la precaución de mantener la misma temperatura y humedad.
Es fácil imaginar la variabilidad biológica si pensamos por ejemplo que tan ser humano es el que mide 210 cm de altura como el que apenas levanta 142 cm del suelo aunque tengan la misma edad y estado de salud.
Ambos “homo sapiens” pero uno pesa 3 veces más que el otro.
En la temporada 1987 -1988 coincidieron el jugador más alto y el más bajo que han pasado por la NBA, Manute Bol y Tyrone Bogues.
Dos hombres adultos uno con enanismo primordial y otro con acromegalia.
El primero se llama He Pingping y mide 74.6 centímetros. El segundo es Sultan Kösen y se eleva hasta los 246.5 cm.
Estarían situados uno a cada lado del extremo inferior de la campana de Gauss
La mayoría de los productos artesanos tienen una utilidad práctica.
Un objeto artístico como la pintura sobre la muerte de Sócrates, de Jacques Louis David puede simplemente ser un transmisor de ideas o de cultura.
El método científico ha desarrollado herramientas que permiten hacer predicciones.
De 20.000 guitarras fabricadas en serie con los mismos tipos de maderas nobles, cortadas y ensambladas con los mismos procesos hasta lograr las mismas dimensiones y espesores, habrá un porcentaje de ellas,
- -pongamos, por ejemplo, unas 40- con un sonido excepcional,
- de 200 a 400- ( 1 al 2%) con un buen sonido,
- el resto (86 a 95%) de la campana de Gauss con un sonido aceptable ,
- un porcentaje pequeño de sonido mediocre (4 a 10%) y
- un 0,2% , con suerte unas 40 de ellas, tendrá un sonido inaceptable.
La distribución en campana de Gauss o distribución normal se cumple con frecuencia en los procesos estadísticos reales (caracteres fisiológicos como el efecto de un fármaco, sociológicos, como la distribución del consumo, psicológicos como el coeficiente intelectual, nivel de ruido en telecomunicaciones, errores de medición, variables poblacionales, de crecimiento, de biometría, caracteres morfológicos …) de especímenes biológicos.
He Pingping y Sultan Kösen estarían situados uno a cada lado del extremo inferior de la campana de Gauss. El primero fuera de -3σ y el segundo por encima de 3σ.
El punto de inflexión se da en el intervalo μ- σ a μ+. Este intervalo, llamado de confianza contiene el 68,26% de los valores de la distribución.
El intervalo 2 sigma que va de μ-2σ a μ+2σ contiene el 99,74% de las posibilidades.
El conseguir reducir la zona de resultados a la zona azul oscuro (zona de confianza sigma 1, μ±1σ) requeriría desencolar y dedicar tiempo a ajustar al menos el espesor de cada tapa armónica y adherir un número variable de barras armónicas hechas a medida, hasta lograr de esa madera el mejor sonido que pueda conseguirse sin poner en riesgo su integridad.
Hay fabricantes de guitarras en serie que establecen controles de calidad que les permite clasificar sus guitarras en niveles para luego venderlas a aficionados o profesionales, lógicamente a precios diferentes.
Como ya dijimos en un artículo anterior, la guitarra se define como instrumento. Un medio para obtener música.
Una vasija artesana y un recipiente industrial permiten con igual eficacia transportar agua.
Es posible fabricarla con el mismo material y criterio sin que se resienta la calidad del agua.
¿Se resiente la calidad de la música en función de las pequeñas variaciones de densidad, elasticidad, tamaño de los vasos y fibras lignificados de la madera aún siendo de una misma especie?, La respuesta, a la luz de la ciencia es claramente, si.
Una guitarra para estudiar en la intimidad, no necesita un alto volumen sonoro pero si unos requerimientos que permitan al artista incipiente evolucionar.
Un uso diario va a someterla a golpes, rayas, desgaste de las partes exteriores, y si no se procura un mínimo de ergonomía, lesiones en las partes anatómicas más solicitadas por el estudiante. La guitarra ha de resultar cómoda de tocar.
Largos años de trabajo diario harán del practicante un músico especialista en ese instrumento, un artista de la interpretación de las partituras que escribió un compositor.
En la utilizada para un concierto el intérprete, el artista, se juega su prestigio y sus posibilidades de supervivencia. Algunas de las propiedades sonoras deben haberse cuidado hasta los límites de lo conocido.
Actuar como solista ante grandes auditorios requerirá un sonido seductor que no se vea comprometido por el mayor volumen sonoro del instrumento. Será muy valioso aquel instrumento que aporte tan sólo un 1% de ventaja y potencie la personalidad interpretativa del músico.Raramente el esfuerzo se prolongará más de una hora.
Un artesano actual admirador del trabajo de Santos Hernández (1875-1943), fabricará en solitario una guitarra cada 4 meses. Tendrá un control absoluto sobre cada una de las tapas armónicas que desarrolle, sobre el correcto cerrado de la caja, sobre mil detalles que favorezcan el mejor sonido obtenible con unas maderas muy seleccionadas y sometidas a largos procesos de secado.
La calidad de aquellos parámetros productivos influidos por la madera seguirá algo parecido a la campana de Gauss, sólo que de perfil mucho más alto que ancho.
Habrá variables que no puedan alcanzar una altura mucho mayor, De 50 guitarras salidas de la mano de este prestigioso guitarrero madrileño un alto porcentaje estarán en la zona central de la banda μ de la serie anterior. Decimos que el valor de la varianza definida como σ (sigma) al cuadrado será mucho menor.
Tenemos toda la tecnología que no teníamos hace 300 años.
Cientos de universidades se dedican en la actualidad a investigar los violines del “mago de Cremona”, Antonio Stradivari (1644-1737) .
Algunos, sin quitar mérito a la calidad de su trabajo, dicen que fue el frío de esa época lo que hacía de la madera de esos violines algo sumamente especial.
El «mínimo de Maunder» fue un período de frío entre 1645 y 1715 que afectó a Europa, mientras se talaba la madera que Stradivarius habría de utilizar.
Otros dicen que es el barniz, del que se han identificado todos los componentes menos uno.
La verdad es que si el curado de la madera fuera la única causa, ya se habría logrado reproducir la calidad sonora de un Stradivari.
Algunos guitarreros actuales consideran que el mago de la guitarra española es el almeriense Antonio de Torres.
Mientras los científicos encuentran la causa de la calidad del sonido los constructores siguen intentando reproducir su alquimia.
Si se deposita una fina capa de arena, o de limaduras de hierro, sobre una placa de vidrio, metal o sobre la tapa superior de un violín, y mediante un altavoz, se hace vibrar a frecuencias diferentes, se obtienen las llamadas "figuras sonoras de Chladni".

El físico alemán Ernst Florenz Friedrich Chladni 1756 -1827) es considerado el fundador de la acústica, por su trabajo sobre vibración, y el cálculo de la velocidad del sonido para diferentes gases.

Las actuales técnicas de interferometría holográfica, basada en luz láser permiten un estudio más preciso y exhaustivo del comportamiento de los llamados modos o patrones de vibración de las tapas armónicas de diferentes instrumentos.
En teoría sería posible visualizar qué hace diferente a un Stradivarius.

Imágenes para BBC news cedidas por el Dr Bernard E Richardson Departamento de Física de la Universidad de Cardiffe (Gales, UK), Mayo 2011.
Sistema holográfico basado en un láser de Argón de 1Watio y de longitud de onda 514,5 nm.

Las frecuencias en las que van apareciendo los diferentes patrones cambian de una guitarra a otra.
Excepto en ciertas frecuencias como 333, 440, 635, y 880Hz las barras transversales, justo por debajo y por encima de la boca, marcan el límite superior de la zona más activa en cuanto a vibración de la tapa, que abarcaría casi totalmente el lóbulo inferior y su abanico.
Plano de la parte inferior y sistema de varetaje en abanico de una guitarra de Antonio de Torres de 1864
La velocidad de transmisión del sonido desde el puente es tres veces más rápido en el sentido de las fibras de la madera (longitudinal) que en el transversal
Las varetas en forma de abanico pueden contribuir a propagar más rápidamente el sonido transversalmente a toda la superficie del lóbulo inferior.

Guitarra SE 85 de Antonio de Torres, (1817-1892) construida en 1885

Sólo ha podido demostrarse la influencia del abanico, en la vibración de la tapa, a frecuencias muy altas 1.250 y 1450 Hz, fuera del rango de frecuencias que generan las notas de la guitarra (de 82,41 Hz del Mi más grave del bordón 6º al La# a 932,33 Hz, nota más aguda situada en el traste 19 de la primera cuerda.
Sólo los armónicos de las frecuencias fundamentales van a estar en ese rango. Por ejemplo la nota obtenida en el quinto traste de la cuerda 2 es un Re# de frecuencia 311,13 Hz . El primer armónico sería 311,13x2= 622,26 Hz, el segundo 311,13x3 =933,39 Hz. El tercero 311,13 x 4 =1.244,5 Hz . La siguiente nota (Mi=329,63 Hz) tiene un tercer armónico de frecuencia 1.318,52 Hz.
Si se sabe que la llamada “cometa”, el conjunto de barras armónicas en forma de abanico tiene una clara influencia sobre la rigidez de la tapa armónica.
En esta, peculiar guitarra del constructor inglés Paul Fischer la boca elíptica ha sido trasladada a la parte alta del lóbulo superior de manera que cruza el diapasón.
La tapa armónica utiliza un varetaje en rejilla apretada con una distribución similar a la forma (c) en la tabla que puede verse, mas adelante de título, "Modo fundamental de Tapa armónica para diferentes varetajes".
Los modos de vibración se producen a distintas frecuencias y a diferencia de la guitarra tipo Torres, la vibración circular concéntrica se divide primero, transversamente, a la altura del puente para luego hacerlo longitudinalmente.
Son muchos los constructores de guitarras de concierto que han experimentado nuevas soluciones, basadas unas veces en ideas sugeridas por la restauración de grandes instrumentos antiguos, otras en el estudio profundo del abanico y su influencia en la vibración de la tapa, los más osados reubican y redimensionan la boca, o ensayan nuevos barnices, modificaciones en la forma de la caja, nuevos materiales…
 Dos de las innovaciones que más han llamado la atención del mundo de la guitarra fueron las protagonizadas por el australiano Greg Smallman y los constructores alemanes Matthias Dammann y Gernot Wagner.
Dos de las innovaciones que más han llamado la atención del mundo de la guitarra fueron las protagonizadas por el australiano Greg Smallman y los constructores alemanes Matthias Dammann y Gernot Wagner.El primero substituyó el abanico tradicional por una rejilla fabricada con fibra de carbono y madera de balsa.
Los dos siguientes diseñaron la tapa hueca doble, laminada y con núcleo interior de rejilla hexagonal (tipo nido de abeja) de un tipo de composite aeronáutico denominado nómex, obteniendo las mismas características de sonido que una buena guitarra tradicional, pero con un volumen y proyección considerablemente mayores así como una mayor sensación de blandura en la pulsación, que se atribuye a la flexibilidad de la tapa. Algunos guitarreros argumentan que también amplifica los errores de diseño.
La construcción de una tapa doble de este tipo, que se debería llamar con mas propiedad "tapa hueca" consiste en un bocadillo formado por dos láminas exteriores de madera, separadas por un material aligerante. Las paredes de las celdas son de unos 0,2 mm. de espesor; el tamaño de estas es de unos 3,5 mm. entre vértices opuestos y la altura de la capa es de 1,5 mm. Este material es extremadamente ligero, está compuesto de fibra de Kevlar y se desarrolló en principio para ser utilizado como aislante térmico en la confección de trajes y calzado para astronautas.
Las paredes exteriores de la tapa son de unos 0,6 o 0,7 mm. de espesor con lo que el total es de unos 2,7 mm. en la partes mas gruesas, si bien para adaptarlo a los mínimos que se usan en las tapas macizas, se reduce el espesor del Nómex interior en ciertas zonas antes de pegar las capas de madera exteriores.
Al contrario de lo que ocurre en otros sistemas de construcción basados también en el aligeramiento de la tapa, (como por ejemplo en las guitarras de varetas de madera de balsa de la escuela australiana), las tapas con Nómex, según Luis Cepeda, no tienen el característico sonido percusivo de estas, sino que conservan con toda fidelidad el ataque y el timbre de las maderas de las que están formadas.
- Antonio González Cárdenas diseñó el llamado modelo armónico y desarrolló una muy bien valorada guitarra de 8 cuerdas.
- Manuel Cáceres y Vicente Camacho dieron solución a la guitarra de 10 cuerdas y este último desarrolló un doble fondo
- Evelio Dominguez ideó la guitarra arpa.
- Félix Manzanero desarrolló una guitarra sin abanico y con una séptima cuerda en el interior, así como una guitarra elíptica y con la ayuda de un grupo de ingenieros diseñó un aparato para optimizar la tapa armónica, antes de cerrar.
- Ramirez III es el creador de la guitarra con cámara, utilizó aros dobles e introdujo el Cedro Rojo en 1960, hoy una de las maderas preferidas para la tapa armónica.
- Manuel Rodriguez Fernández perfeccionó el puente movible, ya conocido en el siglo XIX, que permite una afinación perfecta.
Según esta gráfica (no muy de fiar, ya que los científicos que estudian el cambio climático no se ponen de acuerdo), Antonio de Torres Jurado (1817-1892) vivió también la llamada pequeña edad de hielo. Las maderas de coníferas del hemisferio Norte, presentan las fibras longitudinales rectas y muy juntas, tanto más cuanto más frio sea el clima. Cuanto más juntas, mejores cualidades sonoras.
Tamaño de la veta, por encima del puente a los mismos aumentos, en dos guitarras, una con tapa armónica de Cedro Rojo y puente de Palosanto de India y otra con Abeto del Cáucaso y puente de ébano. Las dos maderas más comunes para la tapa armónica son: Pino abeto europeo, también llamado Abeto rojo, Picea excelsa o Picea abies
- Fibra muy recta y grano fino
- Densidad 400-500 kg /m3 (440-460-470)
- Coeficiente de contracción total (unitario) Volumétrica: 13-14% (0,45) Tangencial: 9% (0,27-036) Radial 4-4,5% (0,15-0,19)
- Dureza 1,2- 1,6 semidura
- Flexión estática: 65-77 N/mm2
- Módulo de elasticidad: 10.000-12.000 N /mm2
- Compresión axial: 40-50 N/mm2
- Cortante. 5,0-7,5 N /mm2
- Flexión dinámica 4,0-5,0 J /cm2
- Poco durable frente a la acción de los hongos Sensible a los cerambícidos, anóbidos y termitas
- Costa oeste América
- Fibra recta y grano fino
- Densidad: 320-430 kg/m3 (330-370-390)
- Coeficiente de contracción total (unitario) Volumétrica: 7% Tangencial: (0,20-0,24) Radial (0,07-0,09) Dureza 0,9 muy blanda
- Flexión estática: 48-55 N/mm2
- Módulo de elasticidad: 7.400-8.400 N /mm2
- Compresión axial: 29-35 N/mm2 Compresión perpendicular: 1,8 N/mm2(ASTM)
- Cortante. 4,5-6,5 N /mm2
- Flexión dinámica 2,4-3,4 J /cm2
- Imputrescible Durable o medianamente durable a los hongos. Sensible a los cerambícidos, anóbidos y termitas
con E= módulo de elasticidad o módulo de Young en N /mm2 y ρ= densidad. Una vía de innovación explorada en la actualidad se basa en ensayar nuevas especies para la tapa armónica. Entre ellas:
- la Secuoya, (Sequoia sempervirens) ρ=350 Kg/m3 (E= 7.600 N/mm2),
- Sitka (Picea sitchensis), ρ=455 kg/m3 (E=11.030 N/mm2),
- Pícea roja Adirondack, ρ=449 kg/m3 (E=11.100 N/mm2)
- Abeto del Caucaso, (Picea orientalis) ρ=520 Kg/m3 (E=10.500 N/mm2)
- Engelmann Spruce, (Picea engelmannii), ρ=415 kg/m3 (E= 8,970 N/mm2).
- Su fibra es ondulada y su grano es basto o grueso.
- Densidad: 870-900 kg/m3
- Coeficiente de contracción total (unitario)
- Volumétrica:
- Tangencial: 1,0-2,0% (0,23-0,26)
- Radial 0,7% (0,15-0,18)
- Dureza 10,0 muy dura
- Flexión estática: 100-132 N/mm2
- Módulo de elasticidad: 11.000-14.000 N /mm2
- Compresión axial: 55-65 N/mm2
- Compresión perpendicular: 11 N/mm2(ASTM)
- Cortante. 11,0-17,0 N /mm2
- Flexión dinámica - J /cm2
- Imputrescible. Muy resistente a los hongos, cerambícidos y anóbidos y moderadamente resistente a las termitas
El primer modelo considera dos masas, mp (masa del pistón del puente) y ma (masa del pistón de aire).
El puente unido a esa parte de la tapa armónica funcionaría como un pistón rígido de superficie A unido al fondo rígido mediante un resorte de constante de fuerza Kp
La fuerza aplicada sobre el puente proviene del desplazamiento oscilante de las cuerdas que al ser pulsadas originan un movimiento de onda senoidal.
Segunda ley de Newton o Ley de fuerza “Mutationem motus proportionalem esse vi motrici impressæ, fieri secundum lineam rectam qua vis illa imprimitur”. El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime
Isaac Newton (1643-1727) fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de los Philosophiae naturalis principia mathematica,
El concepto anterior puede escribirse de forma matemática: F= m .a
F = Fuerza
m = masa
a = aceleración
Newton analizó el movimiento de un objeto.
La primera cualidad que define al cuerpo es su peso o masa (m). En una unidad de tiempo (t), pongamos 10 segundos, el objeto se ha desplazado x metros.
Su velocidad (v= x/t) es la cantidad de metros que recorre cada segundo.
Un objeto que cae por un plano inclinado parte de v=0 y poco a poco va cogiendo más velocidad.
La aceleración (a) es la variación de la velocidad con el tiempo.
La primera aproximación al tema de la guitarra que se nos ocurre utilizar, se basa en los estudios del médico y físico alemán Hermann Ludwig Ferdinand von Helmholtz (1821 –1894).
Como podemos ver en el siguiente vídeo construía esferas huecas de latón,(una aleación de cobre y cinc elegida por sus cualidades sonoras para fabricar trompetas, tubas, saxofones…), de diferentes diámetros y volúmenes interiores.
Acercando un objeto vibrante o soplando cerca de la abertura, la esfera producía un sonido concreto que depende del volumen interior de la esfera.
Todos hemos oído algo parecido cuando hemos soplado dentro de una botella. Llenándola de agua, (reduciendo su volumen), el sonido es cada vez más agudo.
El resonador de Helmholtz es un recipiente en forma de ampolla hecho de cristal o metal, con una abertura a cada lado, una de las cuales se introduce en el oído, mientras que la otra se orienta en la dirección del sonido que se desea analizar.
Actúa como un filtro que amplifica un único sonido de una frecuencia determinada, que es la nota que se acaba oyendo.
Una onda sonora es una forma de energía. La voz de una soprano puede romper una copa de cristal.
Todo cuerpo físico, pequeño como una copa, o grande como un puente de hormigón, está compuesto por un sistema molecular que vibra a una o varias frecuencias características, llamadas frecuencias de resonancia.
El fenómeno de resonancia se da cuando uno de estos cuerpos capaz de vibrar es excitado por una vibración exterior que coincide con la misma frecuencia de resonancia del cuerpo.
Un vaso de cristal tiene una resonancia natural en la que transmite más eficientemente una onda sonora en movimiento.
Si se pone cerca de la copa un sonido periódico que emita a la frecuencia de resonancia de la copa, ésta empezará a amplificar esa frecuencia mediante vibraciones cada vez mayores.
Debido a las propiedades físicas del cristal, llegara un punto en el que superaremos su elasticidad y resistencia consiguiendo que el cristal se rompa. En este video Ainoha Arteta lo consigue.
El Puente de Tacoma fue terminado en Junio de 1940 y destruido por el viento en Noviembre. Tenía 853 m de largo por 12 de ancho y 2,5 de grueso. Un viento constante de 68 Km/h logró que el puente entrara en resonancia. El resultado tras 1h es el que muestra el vídeo.
Veamos si es posible calcular la frecuencia “teórica” de resonancia natural de la caja de la guitarra.
vs= velocidad del sonido en el aire 343,3 m/s (a 20 °C de temperatura, con 50% de humedad y a nivel del mar) r= radio de la boca de la guitarra. Por razones quizás estéticas el diámetro (2r) de la boca suele ser 85mm. r= 0,085/2=0,0425m El grosor de la tapa armónica varía entre 2,7 y 3,3 mm. Tomaremos lf=0,003 m Con esos datos queda L=0,6r+lf+r= 0,071m El fondo de la guitarra española tiene un grueso uniforme de 2,7 a 2,8 mm El grosor de la caja de la guitarra clásica oscila entre 95 a 100 mm. La guitarra flamenca es algo más baja, 93 a 98 mm Tomaremos el alto de la caja hc (distancia entre tapa armónica y fondo), hc=98-2,8-3 mm= 0,0922m Existe una formula semiempírica que permite calcular la superficie de la tapa armónica de cualquier guitarra, conociendo sus medidas exteriores.
Lc = longuitud del cuerpo
LS = ancho del lóbulo superior
AC= anchura de la cintura
LI = ancho del lóbulo inferior
Con esta fórmula José Luis Romanillos en su libro “Antonio de Torres guitarrero, su vida y obra” ha calculado el área total de las tapas de las guitarras fabricadas por Antonio Torres en su primera y segunda época.
Primera época: oscila entre 960 y 1322 cm2 con un valor promedio de 1258 cm2
Segunda época: oscila de 920 a 1329 cm2 con un valor promedio de 1329 cm2
Tomando como valor S Tapa armónica promedio = 1290 cm2= 0,1290m2 podemos calcular el volúmen
VTapa armónica promedio= STapa armónica promedio.hc= 0,1290x0,0922= 0,0118938 m3 y con esos datos:
No resulta difícil idear hipótesis y ensayar experimentalmente el efecto de modificar el diámetro de la boca o el tamaño de la caja, por ejemplo.
Si las mediciones experimentales coinciden con las que dan las ecuaciones, esta aproximación será correcta en un rango de frecuencias al menos próximo al del resonador de Helmholtz. Pero, claro, una guitarra es algo bastante más complejo que esto.
Analicemos el modelo más simple propuesto para la guitarra (el desarrollado por el australiano Caldersmith, (actualmente constructor de guitarras, http://www.caldersmithguitars.com/) y los daneses Christensen y Vistisen).
Estos autores esquematizan la guitarra en una caja de paredes rígidas con un orificio redondo (boca) y un oscilador llamado armónico simple constituido por una masa mp y un área del pistón “A” junto a un resorte de elasticidad “Kp”.
 Si quitásemos, o tapáramos la boca, podríamos calcular la frecuencia de resonancia de esta caja formada por un pistón unido al puente, con la fórmula deducible de la teoría de osciladores:
Si quitásemos, o tapáramos la boca, podríamos calcular la frecuencia de resonancia de esta caja formada por un pistón unido al puente, con la fórmula deducible de la teoría de osciladores:El cambio de Volumen (∆V, léase incremento de V) de la cavidad es:
A y S son las superficies en m2 de los respectivos pistones. xp y xa los elegimos de forma que representan el desplazamiento positivo por fuera de la caja.
Podemos calcular el incremento de la Presión del aire P, en el interior del sistema utilizando la ecuación que se deduce para compresión adiabática:
en la que se define
Conocemos los siguientes datos:
- vs= velocidad del sonido en el aire 343,3 m/s (a 20 °C de temperatura, con 50% de humedad y a nivel del mar)
- ρ es la densidad del aire 1,205 Kg/m3
- El volumen en reposo del interior de la caja de una guitarra lo hemos calculado antes 0,0118938 m3
Vemos que cualquier pequeña variación de volumen modifica fuertemente la presión del aire en el interior.
Puesto que se define Presión como la fuerza aplicada por unidad de superficie:
Llamando Rp y Ra las resistencias al movimiento respectivo de cada oscilador, podemos escribir un sistema de dos ecuaciones diferenciales.
La ley de Newton indica que:
Cuando los incrementos o intervalos se reducen infinitesimalmente se habla de derivadas
queda:
Quienes están acostumbrados a ver las ecuaciones del movimiento armónico en seguida reconocen que α=μSA coincide con la llamada constante de acoplamiento como muelle de dos osciladores.
La solución o soluciones (al ser de segundo grado, cabe esperar dos soluciones, pero pueden ser iguales) de este sistema de ecuaciones diferencial nos daría la ecuación de los desplazamientos de xp y xa en función del tiempo en relación a las constantes constructivas A, S, Kp, y la fuerza aplicada.
A los autores les interesa más obtener las frecuencias o modos normales de vibración para verificar si las ecuaciones deducidas reproducen la forma y valores que sabemos adoptan experimentalmente, y la medición del nivel de presión sonoro.
Caldersmith en este punto, intenta aproximar la forma que tendría la curva que origina los anillos concéntricos en el lóbulo inferior de la guitarra, para el primer modo de vibración a más baja frecuencia (103Hz en el ejemplo anterior).
Friedrich Wilhelm Bessel (1784 - 1846) fue un matemático alemán, astrónomo, que generalizó las llamadas en su honor funciones de Bessel descubiertas por Daniel Bernoulli.
La representación gráfica de la ecuación de Bessel de primer orden tiene esta forma:
La forma es muy similar pero la curva en el holograma de la guitarra es tridimensional (ejes cartesianos x, y, z) y la función de Bessel que acabamos de definir está en el plano (x,y).
La ecuación de Bessel tiene esta forma:
Г(z) es la función Gamma de Euler.
Para α=0 y α=1 quedarían
Que corresponden a la curva roja y verde de la gráfica anterior.
Jα(x) es la solución a una ecuación diferencial de segundo orden del tipo:
Donde α que en este caso es un número entero (1,2,3…) se llama orden. La anterior se llama función de Bessel de primera especie porque las curvas coinciden en el origen.
Para aproximarnos a la forma de ondas que aparece en los hologramas para 103 Hz, nos basta la curva de orden 0.
La forma de la curva en la dirección paralela al puente sigue la línea roja y la longitudinal al eje de la guitarra sigue la línea azul.
La simplificación que el propone seguiría la curva punteada.
Corresponde a la función coseno.
Un oscilador armónico amortiguado es aquel que, en adición a la fuerza recuperadora dada por la ley de Hooke, experimenta una fuerza de rozamiento viscoso proporcional a la velocidad.
Si este oscilador amortiguado se encuentra sometido a una fuerza externa adicional, en general dependiente del tiempo, se dice que el oscilador está forzado, siendo su ecuación de movimiento:
De entre los posibles tipos de fuerza que se pueden aplicar, la más importante desde el punto de vista físico, es aquella que en sí misma es oscilante, esto es donde la frecuencia de oscilación de la fuerza ω no tiene por qué coincidir con la frecuencia propia del oscilador armónico ωo
El factor de calidad, Q, de un oscilador mide cómo de agudo es el pico de una resonancia.
Se define, en términos de la energía como
donde las cantidades se evalúan en la frecuencia de resonancia ωo.
Gráficamente, para resonancias muy agudas, el factor de calidad es inversamente proporcional al ancho de banda, que es la anchura del pico medido a media altura
Cuanto más estrecho sea el pico, menor es el ancho de banda y mayor es Q
Los creadores de estos modelos matemáticos de la guitarra como caja de resonancia (reflex enclosure) destacan algunos aspectos que tienen las buenas guitarras de concierto.
Christensen y Vistisen analizaron 9 guitarras de afamados luthiers internacionales.
Para 7 de ellas pudieron determinar los llamados factores de calidad Q+ y Q-.
donde f- es la primera frecuencia de resonancia y f+ es la segunda frecuencia de resonancia de la guitarra.
Encontraron que:
Q+= 24,3 ± 5,6 (15,5 a 34,8)
y
Q-= 16,5 ± 6,7 (6,5 a 29).,
Las mejores guitarras tienen altos valores de Q-.
Otra observación es que la relación (A/mp) entre el área equivalente del pistón A y su masa equivalente mp varia entre 14,8 y 1,9. La Presión sonora es directamente proporcional a ese cociente entre el área y la masa.
En el rango de frecuencias bajo (sobre los 300 Hz) la guitarra con el cociente mayor (14,8) es bastante mejor que la que obtiene 1,9.
Un alto cociente, puede obtenerse reduciendo mucho el espesor de la tapa armónica , pero eso baja la resistencia del sistema y baja las frecuencias de los modos más altos, que determinan la respuesta a los agudos.
Los tres cocientes más altos obtenidos por los instrumentos analizados tienen A/mp entre 8,4 y 11,2, lo que probablemente sea una solución de compromiso.
Caldersmith realiza un montaje experimental de una guitarra simplificada al máximo para comprobar algunos parámetros y su importancia pero prefiere no manifestarse sobre el efecto en la calidad sonora del instrumento.
Algunos constructores de guitarras consideran que las matemáticas en la construcción de guitarras ayuda en la medición y comprensión de curvas y ángulos.
Una apreciación de la conexión entre la música y las matemáticas ayuda en el proceso de diseño.
Cada guitarra es diferente, los mejores ajustes realizados de manera correcta dan a cada guitarra un sonido único.
Ver video Maths Careers Ver fuente original
Un análisis más completo, confiamos poder incluirlo en la sección Acústica de la guitarra de este mismo Blogg.















++176+copia.jpg)





































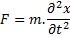



















No hay comentarios:
Publicar un comentario